Understanding Delaunay Triangulation.

I have posted earlier about the Voronoi Diagrams. Well, simlar to that diagram there is another diagram called the Delaunay Triangulation.

The Delaunay triangulation of a collection of point is a set of edges satisfying an "empty circle" property. Empty Circle property specifies that for each edge, we can find a circle containing the edge's endpoints but not containing any other points.

The Delaunay triangulation is the dual structure of the Voronoi diagram in R².

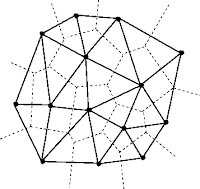Delaunay Triangulation (on top of Voronoi Diagram)

Delaunay From Voronoi

Looking at the above diagram we can clearly see, drawing a line segment between two Voronoi vertices if their Voronoi polygons have a common edge, forms the Delaunay Triangulation. Or, in more mathematical terminology: there is a natural bijection between the two which reverses the face inclusions.

Voronoi From Delaunay

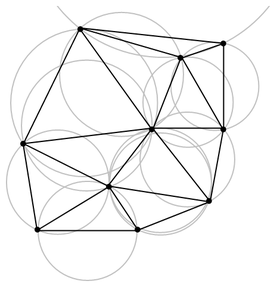
The circumcircle of a Delaunay triangle is called a Delaunay circle and the center of these Delaunay Circles if connected gives the Voronoi Diagrams.

More information of Delaunay Triangulation can be found here : Wikipedia Delaunay Triag.